우리는 단일 회전에 대한 평균을 계산할 때 위의 모든 혜성 핵이 같은 속도로 먼지 입자를 방출한다고 가정했습니다. 우리는 또한 이러한 매개 변수를 수정하면 모든 핵이 동일한 모양과 SFD를 가진 먼지 입자를 방출한다고 가정했습니다. 이러한 가정 하에서 초기 먼지 질량 JFC : HTC-2 : ETC-1 : ETC-2 사이의 비율은 486 : 6 : 19 : 11입니다. 우리는 다음 방법을 사용하여 주어진 β 값에 대해 다양한 입자 연령을 포함하는 IDP 분포를 구성했습니다. . 먼저 100 년마다 먼지 입자의 위치와 속도를 기록하고 각 먼지 입자에서 1000 × wi 입자를 복제했습니다. 우리는 매개 변수 wi에 비례하도록 클론의 수를 설정합니다. 복제 과정에서 우리는 세 개의 궤도 요소 (즉, 반장 축, 편심 및 경사)를 일정하게 유지하고 근일점, 오름차순 노드의 경도 및 각 복제에 대한 평균 이상에 대한 인수를 무작위로 지정했습니다. 결과적으로, 우리는 단일 β 값을 가진 클론과 100 년마다 같은 종류의 혜성 집단으로 구성된 스냅 샷을 만들었습니다.
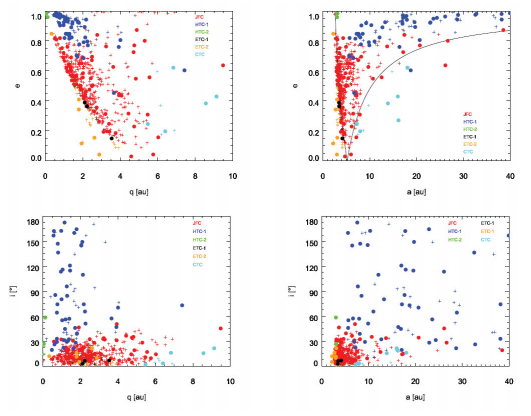
안정된 상태 (즉, 분진 분출이 2 백만 년 동안 지속적으로 발생 했음)를 가정하면, 현재 시대부터 주어진 통합 시간 이후의 분진 입자 기록을 현재 시대 이전의 동일한 시간에 가능한 분출 기록으로 간주했습니다. . 이 가정은 Wiegert et al. (2009). 마지막으로 스냅 샷을 합하여 소스에서 싱크로의 완전한 동적 진화를 포괄하는 IDP 분포를 구성했습니다. 위의 수치 계산 정보를 사용하여 다음과 같은 방법으로 초기 분진 배출 조건을 검증했습니다. 먼지 입자 모양, 질량 밀도 및 초기 SFD에 대한 초기 조건이 주어질 때마다 결과 IDP 구름 복합 모델이 도출되었습니다. 우리는 데카르트 좌표로 3 차원 격자를 만들었습니다. 0.1 au × 0.1 au × 0.1 au 그리드가 행성 간 공간 전체에 구축되었으며 단일 그리드 내에서 주어진 β 값의 먼지 입자 수를 계산했습니다. 다른 β 값의 결과는 주어진 초기 조건에 의해 가중치가 부여되었습니다 (3.3.2 절 참조). 다음 단계로, 모든 단일 그리드 상자 내에서 부분적으로 지수 SFD를 가정하여 그리드 상자에서 IDP의 누적 수, 단면 및 질량 분포를 도출했습니다. 그런 다음 서로 다른 출처 인구의 수를 합한 후 지구 궤도 주변의 SFD를 β = 0.00285로 정규화하고 Gr¨un 등의 관측 SFD와 비교했습니다. (1985), 이는 Pegasus 및 HEOS-2 임무를 통해 획득되었으며 참조 SFD 모델로 널리 적용되었습니다. 우리는 정규화 된 SFD와 관찰 된 β 0.00057 ∼ 0.114 사이의 비율을 조사하고 SFD의 비율이 모든 β 값에 대해 0.5 ∼ 2 사이이면 주어진 초기 조건을 유효한 것으로 취급합니다. 이러한 경우, 비율 로그의 평균 절대 값으로 적합도를 도출했습니다. 마지막으로, 전체 IDP 구름 복합체 모델은 반 태양 방향 (즉, gegenschein)에서 관찰 된 황도광 밝기와 일치하도록 확장되었습니다 (Leinert et al. 1998; Ishiguro et al. 2013). 하위 섹션 3.2.1에서 언급했듯이 가장 큰 먼지 크기를 β = 0.00057로 제한했습니다. 이 컷오프는 전체 단면에 미미한 영향을 미칠 것으로 예상되지만 초기 조건에 따라 전체 질량에 상당한 영향을 미칠 수 있습니다.
'천문학' 카테고리의 다른 글
| 혜성먼지 진화의 상호작용 (0) | 2020.12.31 |
|---|---|
| 행성 먼지의 입자 모양 (0) | 2020.12.31 |
| 혜성먼지의 생성과 방출 (0) | 2020.12.31 |
| 혜성 먼지의 진화 (0) | 2020.12.31 |
| 행성간 먼지입자와 황도광의 비교분석 (0) | 2020.12.31 |




댓글